蓝桥杯算法入门第18讲：线性DP

线性DP（线性动态规划）是动态规划中的一类问题，其特点在于处理的对象是线性结构（如数组、字符串），且状态转移沿着线性顺序进行。特点：

• ️线性结构。处理对象通常是序列或数组，例如字符串、一维数组等。

• ️顺序处理。状态转移按固定方向（如从左到右、从前往后）逐步推进，每个状态仅依赖于前面已计算的状态。

• ️状态维度。状态可以是单维（如dp[i]）或二维（如dp[i][j]），但填充顺序遵循线性规则（如逐行或逐列填充）。️

• ️依赖关系。每个状态的更新通常仅涉及前一个或少数几个状态，而非所有历史状态。

️线性结构。处理对象通常是序列或数组，例如字符串、一维数组等。

️顺序处理。状态转移按固定方向（如从左到右、从前往后）逐步推进，每个状态仅依赖于前面已计算的状态。

️状态维度。状态可以是单维（如dp[i]）或二维（如dp[i][j]），但填充顺序遵循线性规则（如逐行或逐列填充）。️

️依赖关系。每个状态的更新通常仅涉及前一个或少数几个状态，而非所有历史状态。

• ️树形DP。状态转移发生在树结构上，依赖子节点的状态（如二叉树中的路径问题）。

• ️状态压缩DP。通过位运算等技巧压缩状态空间（如旅行商问题）。

• ️区间DP。在区间上进行状态转移，如矩阵链乘法或石子合并问题。

️树形DP。状态转移发生在树结构上，依赖子节点的状态（如二叉树中的路径问题）。

️状态压缩DP。通过位运算等技巧压缩状态空间（如旅行商问题）。

️区间DP。在区间上进行状态转移，如矩阵链乘法或石子合并问题。

下面用一些题目练习线性DP。

2022（0/1背包的方案数）

https://www.lanqiao.cn/problems/2186/learning/

题目描述：将 2022拆分成10个互不相同的正整数之和，总共有多少种拆分方法？注意交换顺序视为同一种方法。

这是标准0/1背包的扩展，求最优的方案一共有多少种。

题解：

这一题其实就是0/1背包：背包容量为2022，物品体积为1~2022，往背包中装10个物品，要求总体积为2022，问一共有多少种方案。

展开全文

与标准背包的区别是：这一题是求方案总数。

定义dp[][][]，dp[i][j][k]表示数字1~i取j个和为k的方案数。下面的分析沿用标准0/1背包的分析方法。从i-1扩展到i，分为两种情况：

（1）k≥i。数i可以要，也可以不要。

要i。从1~i-1中取j-1个数，再取i，等价于dp[i-1][j-1][k-i]。

不要i。从1~i-1中取j个数，等价于dp[i-1][j][k]

合起来：

dp[i][j][k]=dp[i-1][j][k] + dp[i-1][j-1][k-i]

（2）k<i。由于数i比总和k还大，显然i不能用。有：

dp[i][j][k]=dp[i-1][j][k]

下面是代码。

最长公共子序列

https://www.lanqiao.cn/problems/1189/learning/

题目描述：有一个箱子容量为 V（正整数，0≤V≤20000），同时有n个物品（0< n ≤ 30），每个物品有一个体积（正整数）。要求 n 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

输入描述：输入第一行，一个整数，表示箱子容量。第二行，一个整数 n，表示有n个物品。接下来n行，分别表示这n个物品的各自体积。

输出描述：输出一行，表示箱子剩余空间。

题解：

最长公共子序列（Longest Common Subsequence，LCS）：一个给定序列的子序列，是在该序列中删去若干元素后得到的序列。例如：X = {A, B, C, B, D, A, B}，它的子序列有{A, B, C, B, A}、{A, B, D}、{B, C, D, B}等。子序列和子串是不同的概念，子串的元素在原序列中是连续的。

给定两个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。最长公共子序列是长度最长的子序列。

用暴力法找最长公共子序列，需要先找出A的所有子序列，然后一一验证是否为Y的子序列。如果A有m个元素，那么A有2m个子序列；B有n个元素；总复杂度大于O(n2m)。

用动态规划求LCS，复杂度是O(nm)。

用dp[i][j]表示序列Ai（表示a1 ,..., ai这个序列，即A的前i个元素组成的序列；这里用小写的a表示元素，用大写的A表示序列）和Bj（表示b1, ..., bj这个序列，即B的前j个元素）的最长公共子序列的长度。dp[n][m]就是答案。

分解为2种情况：

（1）当ai = bj时，已求得Ai-1和Bj-1的最长公共子序列，在其尾部加上ai或bj即可得到Ai 和Bj的最长公共子序列。状态转移方程是：dp[i][j] = dp[i-1][j-1] + 1

（2）当ai ≠ bj时，求解两个子问题：Ai-1和Bj的最长公共子序列；Ai和Bj-1的最长公共子序列。取其中的最大值，状态转移方程是：dp[i][j] = max{dp[i][j-1], dp[i-1][j]}

}cout << dp[n][m];}

蓝桥骑士

最长递增子序列

Longest Increasing Subsequence，LIS

https://www.lanqiao.cn/problems/1188/learning/

题目描述：小明是蓝桥王国的骑士，他喜欢不断突破自我。这天蓝桥国王给他安排了 N个对手，他们的战力值分别为a1, a2, ..., an，且按顺序阻挡在小明的前方。对于这些对手小明可以选择挑战，也可以选择避战。身为高傲的骑士，小明从不走回头路，且只愿意挑战战力值越来越高的对手。请你算算小明最多会挑战多少名对手。1 ≤N ≤3×105

题解：

最长递增子序列：给定一个长度为 n的数组，找出一个最长的单调递增子序列。

例如一个长度为7的序列A={5, 6, 7, 4, 2, 8, 3}，它最长的单调递增子序列为{5, 6, 7, 8}，长度为4。

定义状态dp[i]，表示以第i个数为结尾的最长递增子序列的长度。状态转移方程：

dp[i] = max{dp[j]} + 1, 0< j < i, Aj< Ai

最后答案是max{dp[i]}。

复杂度：j在0~ i之间滑动，复杂度是O(n)；i的变动范围也是O(n)的；总复杂度O(n2)。

下面是复杂度为O(n2)的DP代码。由于本题n≤3×105，提交到OJ会超时。

DP并不是LIS问题的最优解法，有复杂度O(nlogn)的非DP解法。

字符串转换（编辑距离）

https://www.lanqiao.cn/problems/1507/learning/

题目描述：给定两个单词A和B，计算出将A转换为B所需的最小操作数。一个单词允许进行以下3种操作：（1）插入一个字符；（2）删除一个字符；（3）替换一个字符。

输入描述：输入第一行包含一个字符串 S。输入第二行包含一个字符串T。1≤∣S∣,∣T∣≤2×103，保证S、T只包含小写字母。

输出描述：输出一个整数表示答案。

题解：

为方便理解，把长度m的A存储在数组a[1] ~ a[m]，长度为n的B存储在b[1] ~ b[n]，不用a[0]和b[0]。

定义状态dp，dp[i][j]表示A的前i个字符转换B的前j个字符所需要的操作步骤，dp[m][n]就是答案。下图是A=”abcf”，B=”bcfe”的状态转移矩阵。

状态转移方程：

（1）若a[i] = b[j]，则dp[i][j] = dp[i-1][j-1]。例如图中dp[2][1]处的箭头。

（2）其他情况：dp[i][j] = min{dp[i-1][j-1], dp[i-1][j], dp[i][j-1]} + 1。例如图中dp[4][2]处的箭头。dp[i][j]是它左、左上、上的三个值中的最小值加1，分别对应以下操作：

1）dp[i-1][j]+1，删除，将A的最后字符删除；

2）dp[i][j-1]+1，插入，在B的最后插入A的最后字符；

3）dp[i-1][j-1]+1，替换，将B的最后一个字符替换为A的最后一个字符。

复杂度：O(mn)。

过河卒（网格图上的DP）

https://www.lanqiao.cn/problems/755/learning/

题目描述：棋盘上 A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。棋盘用坐标表示，A点(0, 0)、B点 (n,m)，同样马的位置坐标是需要给出的。1≤n,m≤20， 0≤马的坐标≤20。

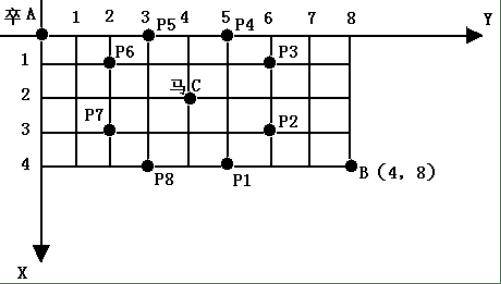
输入格式：一行四个正整数，分别表示 B点坐标和马的坐标。

输出格式：一个整数，表示所有的路径条数。

题解：

统计路径条数，看起来是个搜索题，可以用DFS求解。把马的控制点标记为不能走，绕过它们。不过，用DFS搜索的路径数量是天文数字，肯定超时。

在小学上过奥数的都知道，这题应该用“标数法”，就是在每个坐标点上记录能走的路径条数。

标数法实际上就是DP的递推。定义状态dp[][]，dp[i][j]表示卒走到坐标(i, j)时能走的路径条数。如果不考虑马的控制点，有：

dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

也就是(i, j)点的路径条数等于它上面和左边的路径条数之和。这就是小学奥数的“标数法”的原理。

本题的限制条件是马的控制点，只要令控制点的dp[i][j] = 0即可，即这个点上无路径。

代码第8、9行用了一个小技巧，把坐标加2，这样能防止马的控制点越界。

因为结果是个极大的数字，所以第3行定义为long long。读者编码前可以思考long long是否够用，如果不够用就要用高精度了。不过，也可以先编码，然后用题目要求的最大的n=m=20试试，如果够用就可以了。

砝码称重

https://www.lanqiao.cn/problems/1447/learning/

题目描述：你有一架天平和 N个砝码，这N个砝码重量依次是 W1, W2, · · · , WN。请你计算一共可以称出多少种不同的重量？注意砝码可以放在天平两边。

输入描述：输入的第一行包含一个整数 N。第二行包含N个整数：W1, W2, W3, · · · , WN。

输出描述：输出一个整数代表答案。

题解：

把问题抽象为：给定n个正整数，从中选出若个数字组合，每个数字可以加或者减，最终能得到多少种正整数结果。用DP求解。

DP状态定义： dp(i, j) 表示前i个数字选择若干个加或者减，能否获得和为j。

DP状态转移方程：

dp(i, j) = dp(i−1, j)∣dp(i−1, j−wi)∣dp(i−1, j+wi)

状态转移方程中有三种情况：

dp(i-1, j)：表示不用第i个数字，和为j；

dp(i-1, j-wi)：表示用第i个数字，且做减法，等价于用i-1个数字实现j-wi；

dp(i-1, j+wi)：表示用第i个数字，且做加法，等价于用i-1个数字实现j+wi。

数字三角形

https://www.lanqiao.cn/problems/505/learning/

题目描述：图中给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

输入格式：输入的第一行包含一个整数 N (1 < N ≤ 100)，表示三角形的行数。下面的N 行给出数字三角形。数字三角形上的数都是0 至100 之间的整数。

输出格式：输出一个整数，表示答案。

题解：

本题要求向左走的次数与向右走的次数差值不超过1，当到达最后一层时，一定是落在中间位置。如果层数是奇数，最后一层落在正中间元素上，如果层数是偶数，最后一层落在第N/2或第N/2+1个元素上。

定义状态dp[][]，dp[i][j]表示从顶部到第i层横向第j个数，最大路径和。它只能从上一层的左边或右边转移而来。

子串简写

https://www.lanqiao.cn/problems/3514/learning/

问题描述：程序猿圈子里正在流行一种很新的简写方法：对于一个字符串，只保留首尾字符，将首尾字符之间的所有字符用这部分的长度代替。例如internationalization简写成i18n，Kubernetes（注意连字符不是字符串的一部分）简写成K8s, Lanqiao简写成L5o等。

在本题中，我们规定长度大于等于K的字符串都可以采用这种简写方法（长度小于K 的字符串不配使用这种简写）。

给定一个字符串S和两个字符c1和c2，请你计算S有多少个以c1开头，c2结尾的子串可以采用这种简写？

输入：第一行包含一个整数 K。第二行包含一个字符串S和两个字符c1和c2。

输出：一个整数代表答案。

题解：

这是一道典型的DP题目，符合DP的特性“重叠子问题”、“最优子结构”。

定义状态dp[]：dp[i]表示到s[1]~s[i]中首字母c1出现的次数。

DP转移：遍历s时，若出现尾字母c2，那么答案累加dp[i - k + 1]。只需遍历一次字符串，计算复杂度为O(n)。

也有队员认为这个方法与前缀和有关。不过，按动态规划来理解更恰当一些。

接龙数列

https://www.lanqiao.cn/problems/3512/learning/

问题描述：对于一个长度为K的整数数列：A1, A2, . . . , AK，我们称之为接龙数列当且仅当Ai的首位数字恰好等于Ai−1的末位数字(2 ≤ i ≤ K)。例如12，23，35，56，61，11是接龙数列；12，23，34，56不是接龙数列，因为56的首位数字不等于34的末位数字。所有长度为1的整数数列都是接龙数列。现在给定一个长度为 N 的数列A1, A2, . . . , AN，请你计算最少从中删除多少个数，可以使剩下的序列是接龙序列？

输入：第一行包含一个整数N。第二行包含N 个整数A1, A2, . . . , AN。

输出：一个整数代表答案。

题解：

本题是求最值，考虑用DP求解。

读数列时，把数看成字符串，读n个字符串，字符串只包含’0’~ ’9’这十个字符。对每个字符串来说，影响接龙的是它的第一个和最后一个字符。

题意很明显：逐一处理n个字符串，每读入一个新的字符串，就更新最长接龙序列的长度。

如何设计DP状态？不假思索的思路是定义dp[i]为到第i个字符串时，最长接龙序列的长度。用这个状态定义是否能得到状态转移方程？请读者思考。

设当前已经处理好了1 ~ i-1个字符串，并得到了最长的接龙序列长度。但是这个最长的接龙序列到底是哪些字符串组成的，很难记录。而且这个最长的接龙序列包含的字符串可能和新读的第i个字符串没有关系。

下面详细分析题意，设计一种巧妙的DP状态。

前面提到，影响接龙的是字符串的第一个和最后一个字符。当读入第i个字符串时，设它的第一个字符是head，最后一个字符是tail。这个字符串对最长接龙序列长度有无贡献？因为是接龙是接前面某个字符的尾字符，所以只需考虑前面字符串的尾字符。

（1）head是前面某个字符串A的尾字符。此时肯定有贡献，可以和A一起接龙，最长序列长度加1。由于前面可能有多个字符串的尾字符是head，为了形成最长接龙序列，可以用dp[i]记录和更新以‘i’为尾字符的最长接龙长度。此时，第i个字符串的dp[tail] = dp[head]+1。

（2）tail是前面某个字符串的尾字符，此时没有贡献，第i个字符的dp[tail]可以赋值为前面以tail字符为结尾的dp[tail]。

根据以上分析，定义状态dp[]，dp[i]表示以字符‘i’为末尾的最长接龙长度。

状态转移方程，取（1）和（2）的最大值：

dp[tail] = max(dp[tail],dp[head]+1)

下面的代码，只有一个for循环，计算复杂度为O(n)。

【练习题】

LanqiaoOJ：健身5130，苏苏的天魂石3859，小骑士过酸水3852，可构造的序列总数3348，苏苏的01字符串3861，数字排列3355，建造房屋3362，结果为真的序列3650，数字三角形505，跳跃553，包子凑数98，对局匹配107，保险箱3545，奇怪的数3528，蜗牛4985，数组分割3535，合并石子3540，松散子序列3543。

洛谷：最长上升子序列B3637，硬币问题B3635，过河卒P1002，数字三角形P1216，最大字段和P1115，编辑距离P2758，魔术棋子P2049。